내가 바라본 역사의 흐름을 바꾼 17가지의 공식들
각종 이슈게시판에서 세상을 바꾼 17개의 공식들이라는 제목으로 글이 돌아다니더라구요. 조금 잘못된 정보도 돌아다니는 것 같기도 하고 해서 공대생의 입장으로서 한번 나름대로 추가적으로 이야기를 해보려고 합니다. 운좋게도 제가 재학중인 과가 전자과인데다가, 이제는 고학번이라 대부분의 과목을 들은 상태여서 이 글에 나오는 왠만한 공식들은 다 한번쯤 직접 사용을 해봤더군요.. 과는 정말 잘 선택한 듯 싶습니다 ^^;
글 내용을 작성하기 위해 외국 페이지도 한번 참조를 해보았어요.
참조한 페이지의 원문은
The 17 Equations That Changed The Course Of History
http://www.businessinsider.com/17-equations-that-changed-the-world-2014-3
입니다.
수학은 우리 주변에 언제나 있고, 그리고 세계에 대한 이해를 무수한 방법으로 변화시키고 확장시켜나가는 도구입니다. 2013년에 수학자이자 과학자인 Stewart가 세상을 바꾼 17개의 공식들(17 Equeations That Changed World)이라는 책을 출간했습니다. 앞으로 소개할 공식들이 이 책에 나오는 것들이구요.
1) The Pythagorean Theorem
기하학 이해의 중요한 기초입니다. 피타고라스가 남긴 업적중 하나이고, 아마 여기 나오는 공식들 중에서는 제일 처음 접하게 되는 것일 겁니다. 저는 중학교 2학년 때 이 공식을 아마 접했던 것 같은데, 빗변 길이의 제곱은 나머지 두 변의 길이의 각각의 제곱의 합과 같다는 얘기이죠.
특히나 이 공식은 유클리드 기하학과 비 유클리드 기하학을 나누는 중요한 공식이기도 한데요, 곡면의 곡률에 따라 a^2+b^2이 c^2보다 작을 수도 있고 클 수도 있습니다. 지구와 같은 구면 위에서는 a^2+b^2이 c^2보다 크게 되지요. 그런 평면에서는 피타고라스의 공식이 성립하지 않습니다. 피타고라스의 공식이 항상 맞을 것이라고 생각하던 저에게 꽤나 충격을 주었던 사실이에요. ^^
2) Logarithms
로그 공식은 큰 수를 매우 효과적으로 우리가 다룰 수 있게 해줍니다. 일반적으로 밑과 지수라는 두가지의 함수값이 되는데, 위의 수식처럼 밑이 생략된 형태는 10이 밑으로 들어가 있는 것으로 보죠. 이와는 별개로 자연로그라는 것도 있는데 이것은 ln(x)로 표현합니다. 물론 이는 책마다 정의가 다르고 밑이 e인 로그를 그냥 log라고 붙이는 책도 있는 것으로 압니다.
이 공식은 로그끼리의 합은 원래 로그를 취하기 전 수를 곱한다음 로그를 취한 값과 같다는 뜻인데, 유도 자체는 정말 쉽습니다. 수학 1에서 처음 나오는 개념이고, 특히나 데이터 구조와 알고리즘을 배우는 공대생이라면 Big-O 표기법을 하면서 지겹도록 보게 될 log입니다. 왜냐하면 이 로그라는 것의 이면에 포함된 의미 중에, 처리 속도가 상수인 것 다음으로 효과적인 알고리즘이 이 log라는 녀석이기 때문이거든요. O(1) 다음으로 효율적인게 O(log n)이죠. O(n)만큼 걸린 것을 병렬처리 하면 O(logn)이 되기도 하구요.
인간의 시각에서는 일정 크기 이상의 수는 솔직히 와 크다~ 하는 생각 밖에 들지 않는데, 이것을 정량적으로 생각시킬 수 있게 하는 강력한 도구라고 볼 수 있겠습니다.
3) Calculus
드디어 나왔습니다. 문이과를 가르게 되는 파워풀한 공식! 위 식은 지겹도록 보는 미분의 정의이죠. 영어로는 Differential이라고 부르는 이 미분은 특정한 순간에 어떻게 수치가 변하는지 알 수 있게 해줍니다. 쉽게 말하면 한 점의 기울기라고 볼 수 있구요. 이것이 없으면 수학이 돌아가지 않을 정도로 참 위대한 공식입니다. 수학에서는 이것과 적분이 항상 같이 붙어다니는데, 이상하게 이 17가지의 공식들이라고 소개된 것에는 적분에 대한 언급은 따로 없네요. 아마 역개념으로 파생된 것이라고 생각하나 봅니다. 정적분은 사실 그렇지도 않은데..
4) Law of Gravity
머리에 사과맞아서 발견해냈다는 유명한 아이작 뉴턴 경의 공식이죠.
거시적 세계(미시적 세계와는 반대되는.. 특히 여기서 말하는 것은 행성 정도의 질량을 가지는 m1, m2이죠)에서 운동을 잘 예측할 수 있는 공식입니다. 지구와 태양, 지구와 달.. 이것들의 움직임을 저 공식 하나로 예측가능합니다. 대단하지 않나요? 두 물체 사이에 작용하는 힘이 그 사이의 거리의 제곱에 반비례하고, 각각의 물체의 질량에 비례한다는 이야기입니다. 이 공식에 의해 질량이 큰 녀석들 일수록 충돌하지 않고 회전하려면 더 먼 거리를 떨어져 있어야 한다는 것도 자연스럽게 유도되어 나오죠.
물론 현대에 와서는 아인슈타인의 상대성 이론에 의해 이 공식이 조금은 부정확하다고 판명이 났습니다만(광속에 가까이 이동하는 물체들에 대해서 다른 공식을 적용시켜야 함) 그럼에도 아직도 간단하게 예측할 때는 이 공식을 사용하죠. 이제는 더 이상 어느 공식이 맞고 틀리고가 중요한 것이 아닙니다. 어떤 현상을 얼마나 잘 기술할 수 있는 공식이냐가 중요한 것이거든요.
5) The square root of -1
아아, 나왔습니다. 복소수! 제 기억이 맞다면 10-가 에서 배웠던 공식이네요. 실수에서만 한동안 가지고 놀았던 세계가, 2차원적인 복소수로 넘어가게 되는 공식입니다. 간단하게 설명하자면, 일반적으로 x^2 + 4 = 0이라는 식에서의 실수해는 존재하지 않습니다. 어떤 수의 제곱은 무조건 양수이기 때문인데요, 여기서 제곱하면 -1이 되는 수를 생각합니다. 물론 이런 수는 없지만 이런 수가 존재한다고 가정함으로써 많은 현상들을 쉽게 설명할 수 있기 때문에 때로는 이런 비정상적인 가정을 하는 것이죠. 그래서 i라는 수가 탄생합니다. 이 수의 존재를 인정하게 되면, 이제 x^2 + 4 = 0의 식의 해는 2i, -2i가 나오게 됩니다. 이 해는 1차원적인 직선에는 표현할 수 없고, 실수축과 허수축이 동시에 존재하는 2차원적인 평면에서만 그릴 수가 있습니다.
그런데 재미있는 것은 전기전자 분야에서는 i라는 것이 전류를 나타내기 때문에 복소수를 i로 표현하지 않는다는 것입니다. 이쪽 세계에서는 또 j라는 수로 -1을 표현하죠. 하지만 의미하는 바는 같습니다. ^^
6) Euler's Polyhedra Formula
일반적인 공대생이라면 떠오르는 오일러공식은 이게 아니긴 하죠. 아마 오일러 이름을 보고 e^(-jx)=cosx+jsinx를 떠올리시는 분들이 많았을 텐데요, 이 17개의 공식을 선정한 저자는 이것보다 이 입체도형의 꼭지점과 변, 면수의 관계를 정의한 공식이 더 중요하다고 판단했나봅니다.
큐브(육면체)를 예로 들면, 8개의 변, 12개의 꼭지점, 6개의 면으로 이루어져 있죠. 이렇게 되면 V-E+F=2에서 8+6-12=2가 얻어지게 됩니다. 어떤 입방체를 떠올리더라도 이 공식이 만족된다는 게 포인트입니다. 육면체 같은 경우에는 머릿속에서 떠올릴 수 있기 때문에 쉽게 알 수 있지만, 임의의 도형에 대해서의 관계는 이 공식이 없으면 쉽게 예측이 불가능할 수도 있겠습니다.
7) Normal distribution
저는 이 공식을 정말 좋아합니다. 정규분포인데, 어떤 임의의 현상들은 낙타 등모양의 그래프를 따른다는 것이죠. 충분한 수의 시행만 있다면 말이죠. 저 공식을 -무한대부터 +무한대까지 적분하면 1이 나옵니다. 그 적분을 실제로 미적분 공부하면 유도도 하죠. 간단하게 한번 유도해보겠습니다. 제가 좋아하는 거니깐.. ^^
e^(-x^2) = exp(-x^2)의 적분 값을 구하는 것에서 출발합니다. 이것을 구하기 위해서는 약간의 트릭이 필요한데, 바로 이 식의 값을 f(x)로 두고 같은 놈을 한번 더 곱하는 것입니다. 하나는 x이니 다른 하나는 y로 해서 식을 만들면 아래처럼 됩니다.
이건 많이 보던 것이죠. x^2+y^2을 보시면 알겠지만 원과 관련된 거에요. 그렇다면 이 식을 적분하기 위해서는 dr dθ가 들어가는 원과 관련되는 적분으로 치환하는 것이 훨씬 편하겠죠. x^2=y^2=r^2, x=rcosθ, y=rsinθ로 치환합니다. 그러면 위 적분은 exp(-r^2)이라는 간단한 꼴로 표현이 되며 중요한 것은 적분구간이 변합니다. r은 0부터 무한대까지 변하고, θ가 0부터 2파이까지 변하면 그만인 것이죠. 이를 이용해서 풀게 되면 최초 구하려는 식의 값은 루트(2파이)가 됩니다. 그래서 위 정규분포 식이 루트(2파이)를 나누고 있는 것이구요. ^^
정규분포는 큰 모집단에 대해 (N>30) 성립을 하기 때문에 현상을 예측할 때 굉장히 강력하다고 하겠습니다.
8) Wave Equation
파동함수에요. 앞서 나온 미분공식을 활용하여 표현이 되었네요. 이런 식이 공대에서 과목수업을 들으면 굉장히 빈번하게 나옵니다. 결국 공대에서 배우는 것들 중 대부분의 것들은 미분방정식을 풀어야 해가 나오게 되어있는 것들이 많이 있습니다. c는 광속을 의미하고 u는 파동함수 자체를 의미하며, t는 시간, x는 변위가 되겠네요. 결국 파동함수에 대한 2차 도함수가 시간과 변위에 대한 두가지로 얻어지는데, 이 두가지가 광속의 제곱이라는 계수로 연관되어 진다는 것입니다. 파동함수는 마찬가지로 현상을 예측하는데 쓰이는데, 음악이나 물결파, 이런 곳들에서 사용되지요.
이렇게만 얘기하면 사용범위가 한정될 것 같지만 현대물리에서 굉장히 중요한 공식중 하나입니다. 왜냐면 물질이라는 것이 이중성을 가지고 있기 때문에, 물질을 입자로만 보면 안되고 파동으로도 같이 보아야 하기 때문이죠. 전자조차도 입자로 생각되지만 파동성을 가지고 있다는 것이 입증이 되었죠. 이는 매우 오묘한 현상입니다. 뒤에 나오지만 불확정성의 원리라는 것이 여기서 나오는 것이구요..
9) Fourier Transform
신호를 다루는 전자공학도라면 빼놓을 수 없는 공식 중 하나죠. 사실 대부분의 공대에서 공업수학을 하면서 배우고 넘어갈 것입니다. 다른 부분은 몰라도 특히 이 퓨리에 변환은 적어도 할 줄은 알아야 하고 도구처럼 사용해야 하죠. Time Domain에서의 신호가 Frequency Domain에서 어떻게 변환되는지 구할 수 있는 공식이죠. 시간의 함수로 표현되는 함수에다가 exp(-j2πtf)를 곱하면 신기하게도 주파수로 표현할 수가 있습니다. 이것은 exp(-j2πtf)라는 놈이 사실 원을 나타내기 때문이구요. ^^ 함수를 원 위에다가 올려놓는 것이니.. 이런식으로 변화되는 것이겠죠.
핵심 아이디어는 이것입니다. 복잡해보이는 신호를 여러개의 주파수를 가지는 함수들의 합으로 보겠다는 거죠. 여기서 말하는 주파수가 라디오 주파수의 그 주파수 맞습니다. 통신쪽 전공을 하시는 분들이라면 아마 놓칠만한 함수는 아닌 듯 합니다.
10) Navier-Stokes Equations
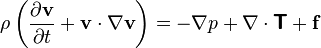
유체의 행동을 기술하는 미분방정식입니다. 아마 기계과에서 많이 사용할 것 같은데.. 저는 있다는 것만 알고 실제로 사용은 해보지 못했네요. 파이프를 통하는 물이라던가, 아니면 비행기날개에 작용하는 공기의 흐름이라던지.. 아니면 담배에서 올라오는 연기 이런 것들을 기술 할 수 있는 식입니다. 현실 세계를 표현하는 물리엔진을 만든다면 아마 이 식이 내부적으로 삽입되어 있겠죠.
11) Maxwell's Equations
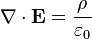
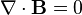
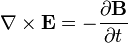
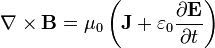
전자쪽을 공부한다면 맥스웰을 모를 수는 없습니다. 그 유명한 맥스웰 방정식 4종 세트입니다. 이 식들은 전기장과 자기장의 관계를 나타내주는 식들이죠. 특이하게도 네 식 모두 기본적으로 벡터방정식들이고, 뒤집어진 삼각형 모양은 Gradient Operator라고 부릅니다. 전기가 흐른다고 하면 기본적으로 자기장이 형성되고, 자기장이 형성되어 이 자기장이 변화하면 전류가 생성되죠. 즉 발전소에서 전기를 생산하는게 이 공식이 없다면 불가능 했을 것이라는 이야기입니다. 전기장이든 자기장이든 변화하면 서로가 생성됩니다. 다만 전기가 흘러서 자기장이 형성되는 것은 자기장이 변화하여 전기가 생성되는 것보다 미미한 효과이기 때문에 일상에서 잘 느끼지 못하는 것이구요.
이 공식이 특별한 이유중 또다른 한가지는 인간이 느끼기에 적합한 사이즈의 공식이라는 것입니다. 뉴턴의 만류인력법칙만 보더라도 그 시점이 너무나 크기 때문에 일상에서 느끼기가 힘든데, 이식은 충분히 느낄만한 크기의 수식이기 때문에 특히나 중요하다고 볼 수 있겠습니다.
12) Second Law of Thermodynamics
열역학 제 2법칙입니다. 닫힌계 (Closed System)에서 앤트로피(Entropy) S는 항상 증가할 수밖에 없다는 것이죠. 앤트로피라는 것은 얼마나 세계가 무질서한지를 나타내는 정도입니다. 간단하게 설명드리자면, 온도는 항상 높은곳에서 낮은곳으로 이동하여 결국에 한 계(System)에서는 온도가 모두 같게 되죠. 이때 온도가 모두 같아지게 되면 더이상 이동이 일어나지 않는 것처럼 보입니다. dS=0이죠. 온도가 변화하고 있을 때는 dS>0입니다. 그렇지만 온도가 평형인 상태에서 온도가 다른 상태로 이동하지는 않습니다. 그래서 dS<0이 될 수는 없습니다. 이 법칙 때문에 우주가 점점 무질서하게 변할 수밖에 없는 것이죠.
이 식이 없었다면 뜨거운 커피가 다시 어는 것을 볼 수도 있었겠지만.. 아쉽게도 그런 일은 일어나지 않습니다. 냉장고라는 것이 없다면요.
13) Relativity
특허청에 근무하던 아인슈타인을 물리학계의 거장으로 만들어버린 공식입니다. 크게 특수 상대성 이론과 일반 상대성 이론이 있는데 이 식은 특수 상대성 이론에서 흘러나온 식입니다. 에너지는 질량과 광속의 제곱의 곱과 같다. 딱히 이공계가 아니라도 많이 들어보셨을 식이죠. 원자폭탄이 강력한 에너지를 내는 이유도 원자폭탄의 질량 감소로 인해 엄청난 에너지가 발생하기 때문입니다. 다시 말씀드리지만 질량과 광속의 곱이 에너지이니까요.
그동안 뉴턴의 공식에 의존하던 물리학계를 바꿔버린 공식이기도 합니다. 이 공식의 출현 이후에 나온 일반 상대성 이론도 과학계를 충격에 빠뜨리기에 충분했죠. 광속은 변하지 않는다! 결국 시간이라는 개념이 상대적이라는 것입니다. Relativity. 이 개념은 철학에까지도 영향을 줍니다. 모든 것은 상대적이다. 이 얼마나 당연한 이야기이지만 모두가 잊고있던 이야기입니까.
광속이 일정하다는 야이기는 광속에 가까이 달릴 수록 시간이 느리게 흐른다는 것입니다. 광속이 일정해야 하니까요. 같은 시간에 더 많이 움직이려면 시간이 멈출 수밖에 없다는 이야기입니다. 이 공식 때문에 사실상 타임머신의 존재는 있을 수 없게 되어버렸지만 각종 SF영화에서는 아직도 타임머신의 존재를 당연하다는 듯이 가지고 나오곤 하죠.
14) Schrodinger's Equation
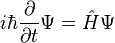
일반물리 아니면 물리II만 들었더라도 한번 쯤은 보았을 공식입니다. 슈뢰딩거의 공식. 확률 개념이 도입됩니다. 아인슈타인이 그렇게 부정하고 싶어했다고 하죠. 신은 주사위놀이를 하지 않는다면서요.. 아인슈타인의 공식은 거시적인 것에 혁신을 가지고 왔다면 슈뢰딩거의 이 공식은 미시적인 것에 혁신을 가지고 왔습니다. 근본적으로 눈에 보이지 않는 입자를 기술하려면 확률 개념을 도입해야 한다는 것이 핵심입니다. 양자역학.. 이쪽 학문은 이 공식이 없었다면 발전하지 못했겠죠. 원자력, 반도체, 레이저 모두 작은 입자들을 다루는 기술이고, 이 공식이 없었다면 탄생되지 못했을 기술들입니다.
15) Information Theory
![H(X) = \mathbb{E}_{X} [I(x)] = -\sum_{x \in \mathbb{X}} p(x) \log p(x).](http://upload.wikimedia.org/math/4/f/0/4f0080f2c78d5b39d6f8ce8dfa076f8e.png)
정보에도 앤트로피가 있다고 보는 공식입니다. 이 연구는 정보를 어떻게 수학적으로 표현할 수 있는지에 대한 기폭제가 되었다고 하네요. 또한 내용을 압축할 때 정보의 손실이 있을 수밖에 없다는 것도 표현을 한다고 하는데.. 솔직히 이쪽 분야는 제 전공이 아닌지라 정확하게는 잘 모르겠네요. ^^; 어쨌든 정보라는 것도 수학적으로 바라볼 수 있게 해 주는 중요한 공식이라고 합니다.
16) Chaos Theory
t에 숫자를 넣어보세요. 한 단계는 다음단계에 어떻게 영향을 미치는지 알 수 있게 해주는 공식입니다. 예를 들면 날씨가 있죠. 날씨라는 것은 결국 이전 단계의 날씨에 영향을 받습니다. 초기값인 x1을 모르더라도, 중간 값인 x_k를 알면 x_k+1을 알 수 있다는 것이죠. 카오스 이론은 이러한 연구를 뒷받침 해줄 수 있게하는 도구입니다.
이와 동시에 중요한 것이 컴퓨터의 발전이죠. 기본적으로 컴퓨터가 없었다면 카오스이론은 아마 발전하지 못했을 겁니다. 엄청난 연산능력을 가진 병렬컴퓨터가 도입되면서 카오스 이론에 입각한 날씨 예측을 할 수 있게 된거죠.
17) Black-Scholes Equation
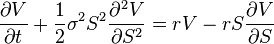
또 미분방정식이네요. 문과생이 이 글을 보면 미분방정식이 뭔지 몰라서 정말 재미없는 글일 것 같습니다. ^^; 앞선 공식들과는 다르게 경제학 공식이네요. V는 옵션가격, S는 시간에 따른 Stock price의 함수, r은 risk-free 이자율(interest rate), o에서 삐져나온 모양의 기호가 있는 이건 시그마라고 읽구요, 이것은 Stock의 불안성이라고 하네요. 경제학에서 수학공식을 활용하여 주식현상을 분석하려는 시도는 계속되고 있고, 그 공식들 중 한가지로 보입니다.
1~17의 식은 재미있게도 실제 식이 세상에 발표된 순서대로 입니다. 현대 사회가 어떻게 변화하고 있는지 보여주는 지표도 되겠네요. 피타고라스의 정리로부터, 현대 경제학 공식까지.. 빠르게 변화하고 있는 세상입니다. 저는 이런 수식들을 볼 때마다 그래도 절반 이상 어떤 의미인지 알 수 있게 해주는 공대에 진학한 것이 정말 행운이라고 생각하고 있습니다. ^^ 결국 기술없는 세상은 없으니까요. 기술에 인문학을 적용 시키는 것이 제 꿈입니다. 예전엔 기술이 한낱 도구라고 생각하는 사람들이 많았는데 이제는 인문학이 기술의 도구가 될 차례입니다. 그런 세상이구요. ^^
'Study and Tip > Study' 카테고리의 다른 글
| [OPIc] 난이도 6-7 AL후기, 수원 영통 (IL->AL) (2) | 2016.04.10 |
|---|---|
| 정보처리기사 필기시험 후기 / 가답안 확인하기 (1) | 2014.08.18 |
| OPIc 대학생 할인 시험접수 방법 (2) | 2014.08.17 |
| [DB] PHP와 MySQL 연동 (2) | 2014.05.16 |
| [DB] 자료테이블을 통해 테이블 구성하기(MySQL 이용) (2) | 2014.04.14 |
| 컴퓨터 활용능력 1급 합격 후기 / 엑세스 암기할 것 정리요약 (4) | 2014.03.01 |
| 영어 단어와 발음을 한번에 공부할 수 있는 사이트 (1) | 2014.02.23 |
| [운전면허] 2종 자동 1일만에 교육, 학과부터 기능합격까지 (0) | 2014.02.16 |
| 컴퓨터 활용능력 1급 독학 필기/실기 시험 후기 (정보처리기능사와 비교) (6) | 2014.02.10 |
| 한국사능력검정시험 무료 인강(인터넷 강의) 추천 (1) | 2014.01.26 |